In this part, we will try to make calculations and estimates on the number of cyclic codes \(C \subset \mathbb{F}_q^{n}\) for a given \(n\). This counting problem is the same as finding the number of factors of \(x^n-1\) in \(\mathbb{F}_q[X]\).
This calculation also relevant for computing the Dedekind-zeta function for cyclotomic fields. Also see this OEIS page for some interesting facts and related sequences.
For simplicity, we will now assume that \(\gcd(n,q)=1\). Later, we will explain why making such a modification is completely feasible.
Let \(\beta\) be a primitive \(n\)th root of unity lying the in the algebraic closure of \(\mathbb{F}_q\) .We know that in the field \(\mathbb{F}_q[\beta]\) the polynomial \(x^n-1\) completely splits as follows.
\[\begin{equation}x^n-1 = (x-1) (x-\beta) ( x - \beta^{2}) \dots (x- \beta^{n-1}) . \end{equation}\]
Now for any root \(\beta^i\) of \(x^n-1\), what are the conjugates of \(\beta^{i}\)? Because we know the structure of the Galois group, we know that the set of conjugates are \(\{ \beta^{i}, \beta ^{iq}, \beta^{iq^{2}}, \dots \}\). This is because the Galois group of a finite field extension is cyclic and generated by the Frobenius isomorphism. Therefore each irreducible factor of \(x^n -1\) looks like
\[\begin{equation} (x-\beta^{i})(x-\beta^{iq})(x-\beta^{iq^{2}})\dots \end{equation}\]
for some \(i\).
Inspired by this, let consider the cyclic group of \(n\) elements \(\mathbb{Z}/n\mathbb{Z}\), written additively. Let \(m_q :\mathbb{Z}/n\mathbb{Z} \rightarrow \mathbb{Z}/n\mathbb{Z}\) be the “multiplication by \(q\)” map. Since \(\gcd(n,q)=1\), we know that this multiplication map is a permutation. More importantly, number of cycles of this permutation are in bijection with the irreducible factors of \(x^n-1\).
Now for for any \(i \in \mathbb{Z}/n\mathbb{Z}\), \(\gcd(i,n) = \gcd(iq,n)\) . So if we write \[\mathbb{Z}/n\mathbb{Z} = \bigsqcup_{d| n} \{ k \in \mathbb{Z}/n\mathbb{Z} \ | \ \gcd(k,n)= d \}, \] then \(m_q\) permutes the elements of each of those disjoint sets. Let us denote each of those disjoint sets as \[\begin{equation}V_d = \{ k \in \mathbb{Z}/n\mathbb{Z} \ | \ \gcd(k,n) = d \}.\end{equation}\] Clearly, \(|V_d| = \varphi(n/d)\), \(\varphi\) being the Euler phi function. As an \(\langle m_q\rangle\)-set, the action of \(m_q\) on \(V_d\) is isomorphic to the action of \(m_q\) on \(\left(\mathbb{Z}/(n/d)\mathbb{Z}\right)^{*}\). Hence the number of cycles of the action of \(m_q\) on \(V_d\) as a permutation is equal to the number of cosets of \(\langle m_q \rangle \subset \left( \mathbb{Z} / (n/d)\mathbb{Z} \right) ^{*}\) which is equal to \({\varphi(\frac{n}{d})}/{ \mathop{\mathrm{ord}}_{\frac{n}{d}}(q ) }\), where \(\mathop{\mathrm{ord}}_{\frac{n}{d}}(q)\) is the order of \(q\) as an element of the multiplicative group \(\left( {\mathbb{Z}}/{\left( n/d \right) \mathbb{Z} } \right)^*\).
With the above discussion, we state the following lemma.
When \(\gcd(n,q) = 1\) , the number of irreducible polynomials that \(x^n-1\) splits in the ring \(\mathbb{F}_q[x]\) is given by \[\begin{equation} \psi_q(n) := \sum_{d | n}^{} \frac{\varphi(d)}{\mathop{\mathrm{ord}}_{d}(q)} . \end{equation}\] Alternatively, we can also write \[\begin{equation}\psi_q(n) = \frac{1}{\mathop{\mathrm{ord}}_n(q)} \sum_{j = 1}^{ \mathop{\mathrm{ord}}_{n}(q) } \gcd(q^j-1,n). \end{equation}\]
The first equation is clear from the discussion before stating the proposition.
The second formula is an outcome of the Burnside’s lemma on the action of the group generated by \(m_q:{\mathbb{Z}}/{n\mathbb{Z}} \rightarrow {\mathbb{Z}}/{ n \mathbb{Z}}\) as a subgroup of the symmetric group \(S_n\).
Let \(G = \langle m_q \rangle\) be this group acting on \(\mathbb{Z}/n\mathbb{Z}\). The size of the group is undoubtedly \(\text{ord}_n(q)\). How many elements are fixed by the element \(m_q^j\) for some \(j\)? That would be the elements of the set \(\{ j \in {\mathbb{Z}}/{n\mathbb{Z}}\ | \ jq^j \equiv_n j \}= \{ j \in {\mathbb{Z}}/{n\mathbb{Z}} \ | \ j(q^j-1) \equiv_n 0\}= \ker(m_{q^j-1})\). There are exactly \(\gcd(q^j - 1,n)\) elements in the kernel of the multiplication map \(m_{q^j - 1} : {\mathbb{Z}}/{ n \mathbb{Z}} \rightarrow {\mathbb{Z}}/{ n \mathbb{Z}}\).
Therefore, by picking up the formula of the Cauchy-Frobenius lemma, we get that the number of orbits is
\[ \frac{1}{ |G|} \sum_{g \in G}^{ }| (\mathbb{Z}/n\mathbb{Z})^{g} | = \frac{1}{\text{ord}_n(q)} \sum_{j=0}^{\text{ord}_n(q) - 1} \gcd(q^j-1,n). \]
The second formula provides computationally a much faster way to calculate \(\psi_q(n)\) when the prime factorization of \(n\) is not known, as compared to the first formula which will require a prime-factorization.
On the other hand, the first formula is more useful for finding an upper bound, as we will see.
If \(\gcd(n,q) \neq 1\), then the following happens. Let \(q = p^{r}\) and \(\gcd(n,q)= p^{s}\) for some \(r,s \in \mathbb{N}^{> 0 }\). In this case \(x^{n} - 1 = (x^{\frac{n}{p^{s}} }-1)^{p^{s}}\) and now \(\gcd(n/p^{s}, q) = 1\). Therefore, the number of factors is now \(\psi_q( n /p^{s})p^{s} = \psi_q(n / \gcd(n,q)) \gcd(n,q)\).
The next proposition is aimed to give an upper bound on \(\psi_q(n)\) as defined in the above lemma.
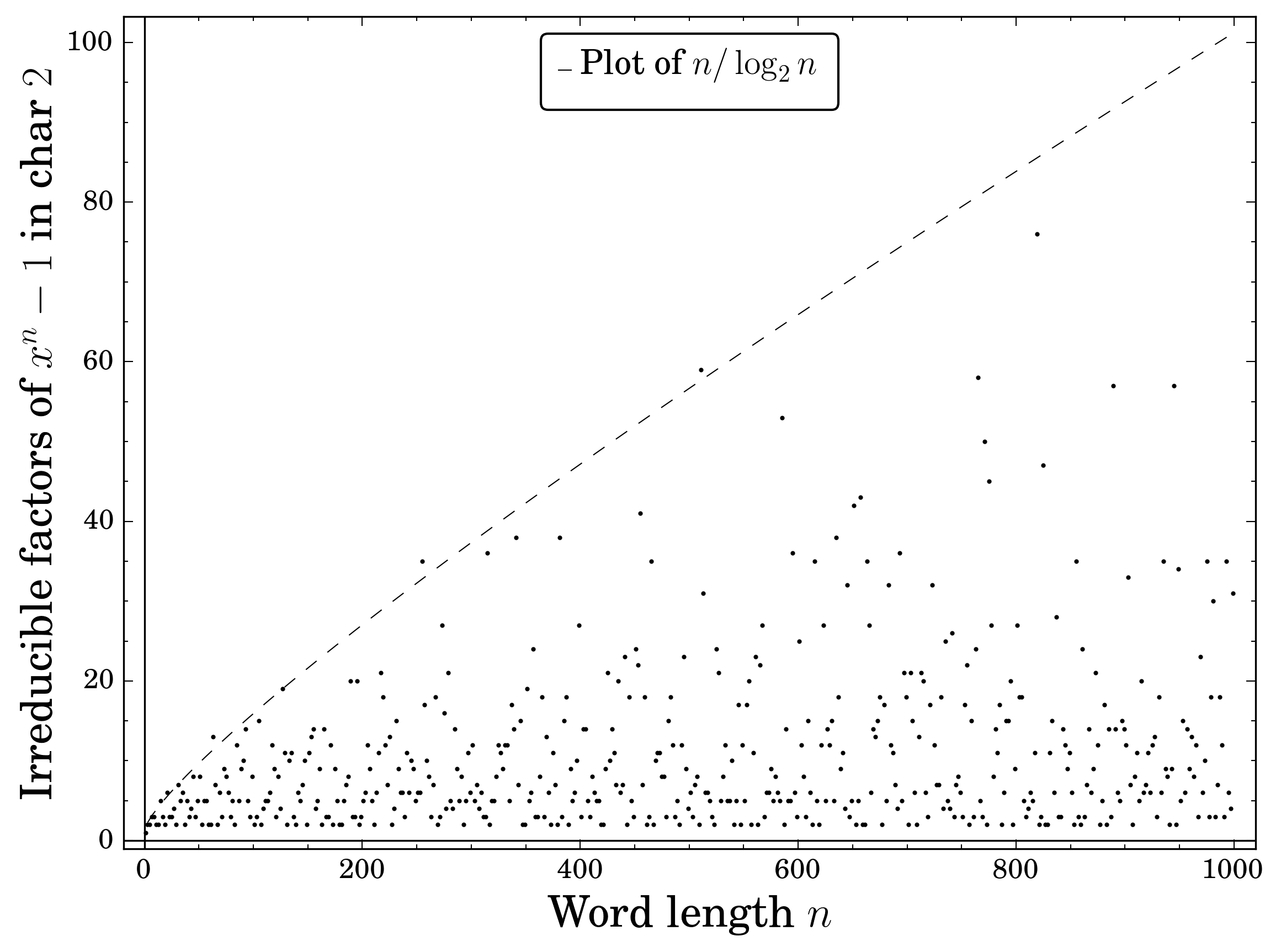
If \(\psi_q(n)\) is as defined in the Proposition , then for any \(C>1\), eventually for large enough values of \(n\) \[\begin{equation}\psi_q(n) < C \frac{n}{\log_qn}.\end{equation}\]
From the preceding discussion, we already have that \[\begin{equation} \psi_q(n) = \sum_{d | n}^{} \frac{\varphi(d)}{\text{ord}_{d}(q)} . \end{equation}\] Now note that for any \(d\), \(\text{ord}_d(q)\) is the smallest exponent \(n\) of \(q\) such that \(q^n \equiv_d 1\). Therefore when \(d \neq 1\), as a natural number \(q^n = 1\) or \(q^n > d\), and since \(q>1\), only the latter is possible. Therefore \(\text{ord}_d(q) > \log_qd\) and therefore \[\begin{equation} \psi_q(n) = \sum_{d | n}^{} \frac{\varphi(d)}{\text{ord}_{d}(q)} \le 1+ \sum_{d | n, d \neq 1}^{} \frac{\varphi(d)}{\log_qd}. \end{equation}\] Let \(\tau(n)\) be the number of divisors of \(n\). It is a classically known result that for any \(\varepsilon > 0\), \(\lim_{n \rightarrow \infty } \frac{\tau(n)}{ n^{\varepsilon}} = 0\). With that in mind, let \(g(n):= \frac{n }{ \tau(n) (\log _q n )^{2}}\) and divide the sum as \[\begin{equation} \sum_{d | n, d\neq 1}^{} \frac{\varphi(d)}{\log_q d} = \sum_{\substack{d | n , d \neq 1 \\ d\le g( n) }}^{} \frac{\varphi(d)}{\log_q d} + \sum_{\substack{d | n , d \neq 1 \\ d > g( n) }}^{} \frac{\varphi(d)}{\log_q d} . \end{equation}\] For the first term, note that \(\varphi(d) \le d\) and therefore \[\begin{equation} \sum_{\substack{ d | n , d\neq 1 \\ d \le g(n) }}^{} \frac{\varphi(d)}{ \log_q d} \le \sum_{\substack{ d | n, d \neq 1 \\ d \le g(n)}}^{} { \varphi(d) } \le \tau(n) \left( \frac{ n}{ \tau(n) \left( \log_q n \right) ^{2}} \right) = \frac{n}{\left( log_q n \right)^{2}}. \end{equation}\] Now for the large divisors, we have that \(d > \frac{n}{\tau(n) \left( \log_q n \right) ^{2}} \Rightarrow \log_qd > \log_qn - \log_q \tau(n) - 2 \log_q \log_q n\). Therefore \(\log_qd > (1+o(1)) \log_q n\) and therefore \[\begin{equation} \sum_{\substack{ d | n , d\neq 1 \\ d > g(n) }}^{} \frac{\varphi(d)}{ \log_q d} \le \sum_{\substack{ d | n, d \neq 1 \\ d > g(n)}}^{} \frac{ \varphi(d) }{(1+o(1)) \log_q n} \le \frac{(1+o(1)) }{\log_q n} \sum_{d | n }^{} \varphi(d) = (1+o(1)) \frac{n}{\log_q n} . \end{equation}\] Since the second term will dominate, we have our result.
For \(q=2\), a comparison of the result with some empirical data is done in the figure below.

This page was updated on November 4, 2021.
Main Page