The following lemma allows easy computation of the Dedekind-zeta function when the field is a cyclotomic extension of \(\mathbb{Q}\).
When \(K=\mathbb{Q}(\mu_{n})\), the \(n\)th cyclotomic field, then we have \[\begin{align} \zeta_K(s) = \prod_{ p \in \mathbb{P } } \frac{1}{\left( 1 - \frac{1}{p^{ s\ \mathop{\mathrm{ord}}_{n_{p}}\ p }} \right)^{\frac{\varphi(n_{p})}{\mathop{\mathrm{ord}}_{n_{p}} \ p}} } , \end{align}\] where \(n_{p} = n p^{-\nu_{p}(n)}\), that is \(n\) with all powers of \(p\) removed.
Since \(\mathcal{O}_{K} = \mathbb{Z}[\mu_{n}]\), we can use Dedekind’s factorization lemma. Let \(\Phi_{n}(X) \in \mathbb{Z}[X]\) be the \(n\)th cyclotomic polynomial. So \[\begin{align} & \Phi_{n}(X) \equiv f_1(X)^{e_1}f_{2}(X)^{e_2}\ldots f_r(X)^{e_r} \pmod{p},\\ \Rightarrow & p \mathcal{O}_{K} = \mathcal{P}_{1}^{e_1} \mathcal{P}_{2}^{e_2} \ldots \mathcal{P}_{r}^{e_r} \end{align}\] for some \(r>0\) and \(e_1,e_2,\cdots,e_r \ge 1\). Now \(\mathop{\mathrm{N}}(\mathcal{P})= p^{\deg f_i(X)}\). What are the roots of \(\Phi_n(X)\)?
If \(p \mid n\), then \(p\) is ramified. In this case, there are no primitive \(n\)th roots of unity in \(\overline{\mathbb{F}}_p\) since \(X^{n} - 1 = (X^{n_{p}}-1)^{p^{\nu_{p}(n)}}\), where \(n_p\) is as in the statement of the lemma. So the set of roots of \(\Phi_n(X)\) in \(\overline{\mathbb{F}}_p\) are the primitive \(n_{p}\)th roots each repeated \(p^{\nu_{p}(n)}\) times.
So we consider the case when \(p \nmid n\). In the algebraic closure \(\overline{\mathbb{F}}_p\), the Frobenious automorphism acts on the primitive \(n\)th roots of unity. We can count the orbits by considering the following multiplication by \(p\) map. \[\begin{align} L_{p} : \left( \frac{\mathbb{Z}}{n \mathbb{Z}} \right)^{*} & \rightarrow \left( \frac{\mathbb{Z}}{n \mathbb{Z}} \right)^{*}\\ x \ \ \ \ \ & \mapsto \ \ \ \ p x. \end{align}\] This map has \(\varphi(n)/\mathop{\mathrm{ord}}_n p\) orbits of size \(\mathop{\mathrm{ord}}_{n} p\). Hence, each \(f_i(X)\) above will have degree \(\mathop{\mathrm{ord}}_{n} p\) and there are \(\varphi(n)/\mathop{\mathrm{ord}}_{n} p\) such polynomials. This gives us all the prime ideals above \(p\) and their norms.
Based on the Euler product above, we can give a series expansion as well when \(K = \mathbb{Q}(\mu_{n})\) as above. We have for \(\Re(s)>1\) \[\begin{align} \zeta_{K}(s) = \frac{a(1)}{1^{s}} + \frac{a(2)}{2^{s}} + \frac{a(3)}{3^{s}} + \frac{a(4)}{4^{s}} + \ldots \end{align}\] where \(a(i)\) is the number of ideals of \(\mathcal{O}_{K}\) that have norm \(i\). We must have \[\begin{align} a(m_1m_2) = a(m_1)a(m_2),\ \ \gcd(m_1,m_2)=1, \end{align}\] and for a prime \(p \in \mathbb{P}\) and \(n_{p}\) as above, we have \[\begin{align} a(p^{m}) = \begin{cases} 0 & \mathop{\mathrm{ord}}_{n_p} p \nmid m \\ \left( \substack{\frac{\varphi(n_p)}{\mathop{\mathrm{ord}}_{n_p} p}+\frac{m}{\mathop{\mathrm{ord}}_{n_p} p} - 1 \\ \frac{m}{\mathop{\mathrm{ord}}_{n_p} p}} \right)& \mathop{\mathrm{ord}}_{n_p} p \mid m \end{cases}. \end{align}\] The non-zero term above is just \[\# \{ (x_1,x_2,\cdots) \in \mathbb{Z}_{\ge 0} ^{\frac{\varphi(n_p)}{\mathop{\mathrm{ord}}_{n_{p}}p}} \ | \ \sum_{i} x_i = \tfrac{m}{\mathop{\mathrm{ord}}_{n_{p}}p}\}.\] Indeed, the tuples \((x_1,x_2,\cdots)\) correspond to the factorization \(\mathcal{I}= \mathcal{P}_{1}^{x_1} \mathcal{P}_{2}^{x_2} \ldots\) where \(\mathcal{I}\) is an ideal such that \(\mathop{\mathrm{N}}(\mathcal{I}) = p^{m}\).
The following sage code computes \(\zeta_{K}(2)\) for any given \(\mathbb{Q}(\mu_n)\) based on the Euler expansion above.
Caution: Not accurate for large \(n\).
MAX = 10000
## Finding largest power of p that divides n
def power_in(n,p):
k=0
while n%p**k==0:
k=k+1
return k-1
s=2
n=100
# Finding Dedekind zeta of Q(mu_n) at s=2
DZ=1.00000000
for p in prime_range(1,MAX):
a=power_in(n,p)
m=n/p**a
ord_mp = multiplicative_order(mod(p,m))
DZ/=(1-1.0/p**(s*ord_mp))**(euler_phi(m)/ord_mp)
print n,DZThe following sage code prints the series expansion \(\zeta_{K}(s)\) in \(\LaTeX\) for any given \(\mathbb{Q}(\mu_n)\) based on the Euler expansion above.
LARGEST = 10000
## Finding largest power of p that divides n
def power_in(n,p):
k=0
while n%p**k==0:
k=k+1
return k-1
s=2
n=210
clist=[]
# Finding Dedekind zeta of Q(mu_n) and putting it in list
for a in range(1,LARGEST):
prod=1
for (p,pow) in factor(a):
n_p=n/p**(power_in(n,p))
ordp = multiplicative_order(mod(p,n_p))
if pow%ordp!=0:
prod=0
else:
prod*=binomial((euler_phi(n_p)/ordp)+(pow/ordp)-1,(pow/ordp))
clist+=[[a,prod]]
# Printing latex output from list
latex_string='\\zeta_{\\mathbb{Q}(\\mu_{'+str(n)+'})}(s)='
NTERMS=6
count=0
for [i,a_i] in clist:
if a_i!=0:
count+=1
if count<NTERMS:
latex_string+='\\frac{'+str(a_i)+'}{'+str(i)+'^s}+'
latex_string+='\ldots'
print latex_string\[ \zeta_{\mathbb{Q}(\mu_{1024})}(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{8^s}+\frac{1}{16^s}+\ldots \]
\[ \zeta_{\mathbb{Q}(\mu_{16})}(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{8^s}+\frac{1}{16^s}+\frac{8}{17^s}+\frac{1}{32^s}+\ldots \]
\[ \zeta_{\mathbb{Q}(\mu_{100})}(s)=\frac{1}{1^s}+\frac{2}{5^s}+\frac{3}{25^s}+\frac{40}{101^s}+\frac{4}{125^s}+\ldots \]
\[ \zeta_{\mathbb{Q}(\mu_{210})}(s)=\frac{1}{1^s}+\frac{48}{211^s}+\frac{48}{421^s}+\frac{48}{631^s}+\frac{24}{841^s}+\ldots \]
\[ \zeta_{\mathbb{Q}(\mu_{30})}(s)=\frac{1}{1^s}+\frac{2}{16^s}+\frac{1}{25^s}+\frac{8}{31^s}+\frac{8}{61^s}+\frac{1}{81^s}+\frac{4}{121^s}+\ldots \]
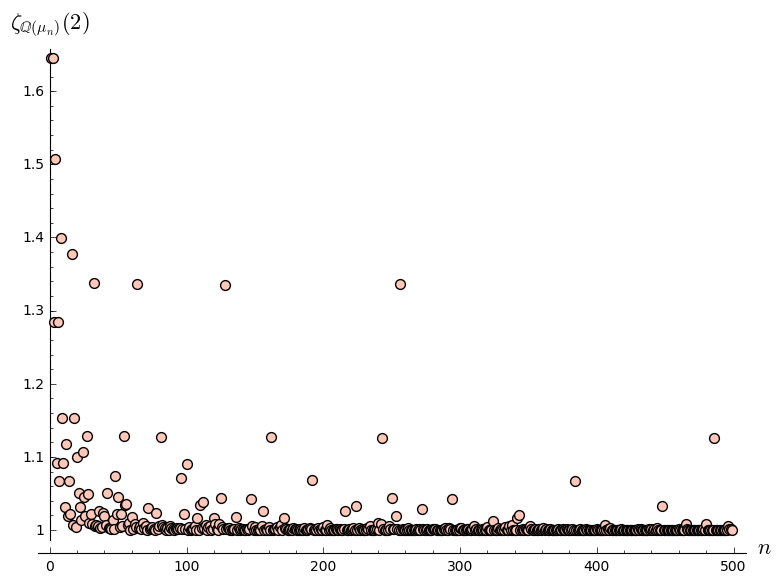
The value of \(\zeta_K(s)\) is bounded for a fixed \(s > 1\) as \(K\) varies across cyclotomic number fields.
Here is some data to support the evidence. On the \(x\)-axis is the value of \(n\). On the \(y\)-axis is the value of \(\zeta_K(s)\) for \(K\) being the \(n\)th cyclotomic number field.
The proof can be found in [1].

This page was updated on February 8, 2024.
Main Page