Lattice packings through division algebras
Presentation by
Nihar P. Gargava
Doctoral student,
Chair of Number Theory,
Section of Mathematics,
École Polytechnique Fédérale de Lausanne,
Introduction
\(\DeclareMathOperator{\R}{\mathbb{R}}\)\(\DeclareMathOperator{\Z}{\mathbb{Z}}\)\(\DeclareMathOperator{\C}{\mathbb{C}}\)\( \DeclareMathOperator{\F}{\mathbb{F}}\) Suppose we have $\{a_1, a_2, ... , a_n \} \in m \Z$ with $a_i \ge 0 $ and suppose that $$\frac{1}{n}\sum_{i=1}^{n} a_i < m.$$
What can we conclude about the numbers $a_i$?
Answer: At least one of them is $0$.
Lemma
(Integrality gap)Let $X$ be a probability space and $\Phi: X\to \R^{\ge 0}$ be a random variable that takes values only in $m \Z$ for some integer $m$.
If $\int_X \Phi < m$, then there exists some $x \in X$ such that $\Phi(x) = 0$.
For our application, we will set $X$ to be a set of lattices.
What is a lattice packing?
Consider $\R^d$ with the standard inner product. A lattice $\Lambda\subseteq \R^d$ is a discrete subgroup such that the quotient space $\R^d / \Lambda$ has a finite induced volume.
Given a lattice $\Lambda$, choose $r > 0$ and consider the open balls $\{ B_{r}\left( v \right)\}_{v \in \Lambda}$ such for any $v_1, v_2 \in \Lambda$, $B_{r}(v_1) \cap B_{r}(v_2) \neq \emptyset \Rightarrow v_1 = v_2$.
Then $(\Lambda,r)$ is called a lattice sphere packing, or simply lattice packing inside $(\R^d, \langle \ , \ \rangle)$.
Packing density of a lattice packing is: \[ \lim_{R \rightarrow \infty} \frac{\mu\left( B_{R}(0) \cap \left( \bigsqcup_{v \in \Lambda} B_{r}(v) \right) \right)}{\mu\left( B_{R}(0) \right)} = \frac{\mu( B_{r}(0) )}{ \mu(\R^d / \Lambda)} \] It is always in the interval $]0,1[$.
Visualizing in $\R^2$
However, note that $2r$ can be at most $$m(\Lambda) = \min_{v \in \Lambda \setminus \{0\}} ||v|| ,$$ otherwise some balls will begin to intersect.
The goal is to maximize packing density. So take $r = \frac{1}{2}m(\Lambda)$. In that case packing density will be equal to $$\frac{\mu( B_{m(\Lambda)/2}(0) )}{ \mu(\R^d / \Lambda)},$$ and is independent of scaling.
To maximize this over all $\Lambda$, it is sufficient to maximize over unit covolume lattices (i.e. \(\mu(\R^d/\Lambda)\) = 1)
Visualizing in $\R^2$
So we somehow find \[ \sup_{\substack{\Lambda \subseteq \R^d \\ \mu(\R^d/\Lambda)=1}} \mu\left(B_{m(\Lambda)/2}(0) \right) \]
\[ = \sup_{ g \in SL_d(\R)} \frac{1}{2^d} \mu\left(B_{m(g \Z^d)}(0) \right) \]
which we use to define our dimensional constant $c_d$ \[ \colon= \frac{1}{2^d} c_d \]
Putting it together, we have \[ c_{d} = \sup\left\{ \mu\left( B_{r}(0)\right) \ | \ r> 0,\exists~g \in SL_d(\R) \text{ and } B_{r}(0) \cap g\Z^d = \{ 0\}\right\}. \]
Clearly, \(~c_d \in~]0,2^d[\), so supremum exists!
Visualizing in $\R^2$
What is known about $~c_d$?
The exact value of the constant $c_d$ is known only for $d = \{ 1,2,3,4,5,6,7,8,24\}$. For other $d$, we want to understand the asymptotic behaviour. In this talk, we will only focus on lower bounds.
Some asymptotic lower bounds for large dimensions
| Lower bound | Contribution of | Dimensions covered |
|---|---|---|
| $c_d \ge 1$ | Minkowksi (1896) | $\forall ~d \ge 1$ |
| $c_d \ge 2(d-1)$ | Ball (1992) | $\forall ~d \ge 1$ |
| $c_{4n} \ge 8.8n$ | Vance (2011) | $d=4n , n \ge 1$ |
| $c_{2\varphi(n)} \ge n$ | Venkatesh (2013) | $d=2\varphi(k)$ for some $k$ |
Since $\lim \inf \left( \frac{\varphi(n)}{n} \log \log n\right) = e^{- \gamma}$, the last bound is the best lower bound (among these, and overall) on $c_d$ in infinitely many dimensions. The first dimension where it outperforms all others in this list is $d=960$.
Explicit lattice constructions can help us only upto $d \le 300$.
(Ball, 1992) , the lower bound is as indicated.
(Vance, 2011) , using a probabilistic argument on lattices that lie in vector-space over quaternion division algebra. Works only when $4 \mid d$.
(Venkatesh, 2013) , using a probabilistic argument on lattices that lie in $(K \otimes_\mathbb{Q} \mathbb{R})^2$, $K$ is a cyclotomic field.
(G., 2021) , using a probabilistic argument on lattices that lie in $(D \otimes_\mathbb{Q} \mathbb{R})^2$, $D$ is a division algebra over $\mathbb{Q}$.
Comparison of bounds
Theorem
(G. 2021)Let $D$ be a finite-dimensional division algebra over $\mathbb{Q}$. Let $\mathcal{O} \subseteq D$ be an order in $D$ and $G_{0} \subseteq \mathcal{O}$ be a finite group embedded in the multiplicative group of $D$. Then if $d=2\dim_{\mathbb{Q}}D$, then \begin{align} c_{d} \ge \# G_{0}. \end{align}
To recover Venkatesh's result, set $D=\mathbb{Q}(\mu_n)$, $\mathcal{O} = \mathbb{Z}[\mu_n]$ and $G_0 = \langle \mu_n \rangle$. Hence, this gives \begin{align} c_{2 \varphi(n)} \ge n \end{align}
The cherrypicked sequence of Venkatesh achieves an asymptotic growth of $O( d \log \log d )$. This is achieved by setting $K$ as the $n$th cyclotomic field where $n=\prod_{p < N} p$.
The new result provides more freedom to cherrypick sequences. Instead of choosing a sequence of cyclotomic fields, we can now choose sequences of $\mathbb{Q}$-divison algebras. However, no such sequence will be able to give an asymptotic result strictly better than $O( d \log \log d )$. Improvements in individual dimensions is still possible, as shown before.
The probabilistic method
Recall:
To show $c_d \ge M$, we must prove the existence of $g \in SL_d(\R)$ such that the origin centered ball $B$ with $\mu(B) = M$ has $g \Z^d \cap B = \{0\} $
This is an optimization problem on the space \[ X_d:= \{ \Lambda \subset \mathbb{R}^{d} | \ \mu(\mathbb{R}^{d} / \Lambda) = 1 \} = \{ g\Z^d \ | \ g \in SL_d(\R) \} \]
\[ \simeq SL_d(\mathbb{R})/SL_d(\mathbb{Z}). \]
A priori, this is a bijection of sets. But now we can pull back the topology and the measure from $SL_d(\R)/SL_d(\Z)$.
$SL_d(\R)$ has the topology of a locally compact group.
$SL_d(\R)$ is unimodular. $SL_d(\Z)$ is a discrete subgroup inside $SL_d(\R)$ and therefore there is a unique left $SL_d(\R)$-invariant measure on $SL_d(\R)/SL_d(\Z)$.
Proposition
There exists a unique (upto scaling) natural measure on $SL_d(\R)/SL_d(\Z)$, left-invariant under $SL_d(\R)$ action on cosets.
Furthermore, $SL_d(\mathbb{R})/SL_d(\mathbb{Z})$ under this has a bounded total measure.
This gives us a probability space. Hence we can talk about random unit covolume lattices.
Lattice-sum function
Consider a bounded measurable function with compact support $f:\R^d \rightarrow \R$.
e.g. the indicator function of a ball.
With this, we can now construct the lattice-sum function $\Phi_f(\Lambda): X_d \rightarrow \R$, given as \[ \Phi_f(\Lambda) = \sum_{v \in \Lambda \setminus \{ 0\}}^{} f(v).\]
Since we can generate random lattices, we can talk about the expected value of $\Phi_f(\Lambda)$.
Let us try to do this experimentally! Let us sample over a set $S \subseteq X_d$ of lattices.
So we see that it is almost the integral.
Visualizing in $\R^2$
What we are empirically confirming is the following.
Theorem
(Siegel, 1945)Suppose $f:\mathbb{R}^{d} \rightarrow \mathbb{R}$ is a compactly supported bounded measurable function. Then, the following holds. \begin{align} \int_{X_d} \Phi_f = \int_{SL_d(\mathbb{R})/SL_d(\mathbb{Z})}^{} \left( \sum_{v \in g \mathbb{Z}^{d} \setminus \{ 0\}}^{}f(v) \right) dg = \int_{\mathbb{R}^{d}}^{} f(x) dx, \end{align} where the $dx$ on the right-hand side is the usual Lebesgue measure on $\mathbb{R}^{d}$ and $dg$ is the unique $SL_d(\mathbb{R})$-invariant probability measure on $SL_d(\mathbb{R})/SL_d(\mathbb{Z})$.
But as you saw that for any $\Lambda \in X_d$, when $f$ is the indicator of a ball, we must have $\Phi_f(\Lambda) \in \{0,2,4,6,...\}$. That's because balls are symmetric. $$v \in \text{supp}(f) \cap ( \Lambda \setminus \{0 \}) \Rightarrow -v \in \text{supp}(f) \cap ( \Lambda \setminus \{0 \}).$$
If $f$ is the indicator function of a ball of volume $2- \varepsilon$, then this tells us that for any dimension $d$ $$\int_{X_d} \Phi_f = 2 - \varepsilon$$
Conclusion: There exists some lattice $\Lambda \in X_d$ such that $\Phi_f(\Lambda) = 0$. That is, there is some lattice of unit covolume that intersects trivially with an origin centered ball of volume $ 2 - \varepsilon$.
Another conclusion: $c_d \ge 2$ for all dimensions $d$!
Here we used a symmetry of $\{\pm 1\}$ under which the ball and the lattice are invariant. Both Venkatesh and the new result use this idea.
Venkatesh's approach was to work with larger a larger group, namely $\Z/n\Z$. For the new result, the symmetries are even bigger and non-commutative.
Venkatesh's lower bound
The idea is to take a nice enough subcollection $Y_d \subseteq X_d$ of lattices and average the lattice-sum function $\Phi_f$ over them.
Define the set $Y_d$ as $$Y_d = \left\{ \left[ \begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\right] \mathcal{O}_K^2 \ | \ a,b,c,d \in K_{\R} = K\otimes \R , ad-bc =1_{K_{\R}} \right\}.$$
In conventional notation, this is just $$Y_d = \{ g ( \mathcal{O}_K^{\oplus 2} ) \ | \ g \in SL_2(K_{\R}) \} \simeq SL_2(K_\mathbb{R} ) /SL_2(\mathcal{O}_K). $$
Again, with this bijection, we will make $Y_d$ a topological space. With a bit of work, we can also show that $Y_d$ has a finite measure with respect to the natural left $SL_2(K_{\R})$-invariant measure.
$Y_d$ can be give probability measure. But why make such a $Y_d$?
Note that whenever $a,b,c,d \in {K}_{\R}$, we have that $$ \left[ \begin{matrix} a & b \\ c & d \end{matrix}\right]\left[ \begin{matrix} \mu_n & 0 \\ 0 & \mu_n \end{matrix}\right]=\left[ \begin{matrix} \mu_n & 0 \\ 0 & \mu_n \end{matrix}\right]\left[ \begin{matrix} a & b \\ c & d \end{matrix}\right]$$
And if $x,y \in \mathcal{O}_K$ and if $r \notin n \Z$, we have that $$ \left[ \begin{matrix} \mu_n^r & 0 \\ 0 & \mu_n^r \end{matrix}\right]\left[ \begin{matrix} x \\ y \end{matrix}\right]=\left[ \begin{matrix} x \\ y \end{matrix}\right] \Rightarrow x=y=0.$$
Putting the two together implies that for each $g\in SL_2(K_{\mathbb{R}})$, $g(\mathcal{O}_K^{\oplus 2})$ is invariant under the cyclic group action of $\langle \mu_n \rangle$, and the action has full orbits on the non-zero points of the lattice.
So if $f$ is the indicator function of an origin-centered ball with respect to a quadratic form that is invariant under $\langle \mu_n \rangle$, we have that $\Phi_f(\Lambda) \in \{0,n,2n,3n,4n,\ldots\}$ for $\Lambda \in Y_d$. Such a quadratic form always exists by averaging!
Venkatesh proves the following analogue of Siegel's theorem.
Theorem
(Venkatesh 2013)Let $d = 2\varphi(n)$. Suppose $f:K_{\mathbb{R}}^2 \rightarrow \mathbb{R}$ is a compactly supported bounded measurable function. Then, the following holds. \begin{align} \int_{Y_d} \Phi_f = \int_{SL_2(K_\mathbb{R})/SL_2(\mathcal{O}_K)}^{} \left( \sum_{v \in g \mathcal{O}_K^{\oplus 2} \setminus \{ 0\}}^{}f(v) \right) dg = \int_{\mathbb{R}^{d}}^{} f(x) dx, \end{align} where the $dx$ on the right-hand side is that Lebesgue measure on $\mathbb{R}^{d}$ that makes $\mathcal{O}_K^{\oplus 2}$ of unit covolume and $dg$ is the unique $SL_2(K_\mathbb{R})$-invariant probability measure on $Y_d$.
Conclusion: By setting $f$ as the indicator function of a ball in a suitable quadratic form, we conclude that there exists some lattice $\Lambda \in Y_d$ such that $\Phi_f(\Lambda) = 0$. That is, there is some lattice of unit covolume that intersects trivially with an origin centered ball of volume $ n - \varepsilon$.
Another conclusion: $c_{2 \varphi(n)} \ge n$ for all $n$!
Using division algebras
The division algebra case is on similar lines.
Let $D$ be a finite-dimensional division algebra over $\mathbb{Q}$. Let $\mathcal{O} \subseteq D$ be an order in $D$. We work in $d = 2 \dim_{\mathbb{Q}} D$ dimensions. Define $D_{\R}= D \otimes_\mathbb{Q} \R$.
$$Y_d = \{ g ( \mathcal{O}^{\oplus 2} ) \ | \ g \in SL_2(D_{\R}) \} \simeq SL_2(D_\mathbb{R} ) /SL_2(\mathcal{O}). $$
Here
$$ SL_2(D_{\R}) = \left\{ \left[ \begin{matrix} a & b \\ c & d \end{matrix}\right] \ | \ \left[ \begin{matrix} x \\ y \end{matrix}\right] \mapsto \left[ \begin{matrix} ax + by \\ cx + dy \end{matrix}\right] \text{ is a measure preserving map on } D_{\R}^{\oplus 2} \right\}$$
$Y_d$ consists of lattices that are invariant under diagonal right-multiplication by units in $\mathcal{O}$ $$ g ( \mathcal{O}^{\oplus 2} ) = g ( \mathcal{O}^{\oplus 2} ) \left[ \begin{matrix} \mu & 0 \\ 0 & \mu \end{matrix}\right] , \text{ for any } \mu \in \mathcal{O}^{*} $$
And if $x,y \in \mathcal{O}$ and if $ \mu \in \mathcal{O}^{*} \setminus \{ 1_{D}\}$, we have that $$\left[ \begin{matrix} x \\ y \end{matrix}\right] \left[ \begin{matrix} \mu & 0 \\ 0 & \mu \end{matrix}\right]=\left[ \begin{matrix} x \\ y \end{matrix}\right] \Rightarrow x=y=0.$$
Theorem
(G. 2021)Let $d = 2\varphi(n)$. Suppose $f:D_{\mathbb{R}}^2 \rightarrow \mathbb{R}$ is a compactly supported bounded measurable function. Then, the following holds. \begin{align} \int_{Y_d} \Phi_f = \int_{SL_2(D_\mathbb{R})/SL_2(\mathcal{O})}^{} \left( \sum_{v \in g \mathcal{O}^{\oplus 2} \setminus \{ 0\}}^{}f(v) \right) dg = \int_{\mathbb{R}^{d}}^{} f(x) dx, \end{align} where the $dx$ on the right-hand side is that Lebesgue measure on $\mathbb{R}^{d}$ that makes $\mathcal{O}^{\oplus 2}$ of unit covolume and $dg$ is the unique $SL_2(D_\mathbb{R})$-invariant probability measure on $Y_d$.
To get packing bounds, fix a finite subgroup $G_0 \subseteq \mathcal{O}^*$ to act diagonally on the right of $\mathcal{O}^{\oplus 2}$. Choose $f$ to be the indicator function of a ball invariant under the right action of $G_0$. Then $\Phi_f(\Lambda) \in \{0, |G_0|, 2|G_0|, \dots\}$ for all $\Lambda \in Y_d$.
Conclusion: We get the bounds $$c_{2 \dim_{\mathbb{Q}} D} \ge \# G_0.$$
Let $(G_{0},\mathcal{O}, D ) $ be as finite subgroup inside an order inside a $\mathbb{Q}$-division algebra respectively. Then there exists a lattice packing in dimensions $d= 2\dim_{\mathbb{Q}} D$ whose packing efficiency is at least $\frac{1}{2^{d}} ( \#G_{0} )$.
Note that the following tightening can be done once we have a tuple $(G_{0},\mathcal{O},D)$. When $D$ is a $\mathbb{Q}$-division algebra, the $\mathbb{Q}$-span of $G_{0}$ in $D$ is also a division algebera. Let $\mathbb{Z}\langle G_{0}\rangle \subseteq \mathcal{O}$ be the $\mathbb{Z}$-span of $G_{0}$, then we get that $(G_{0},\mathbb{Z}\langle G_{0}\rangle ,\mathbb{Q}\langle G_{0}\rangle )$ is another tuple that gives us a lower bound.
So we only need to find finite subgroups $G_0$ that live in some $\mathbb{Q}$-division algebra $D$ and we can get the rest.
Fortunately, there exists a complete classification of such finite subgroups due to Amitsur, 1955.


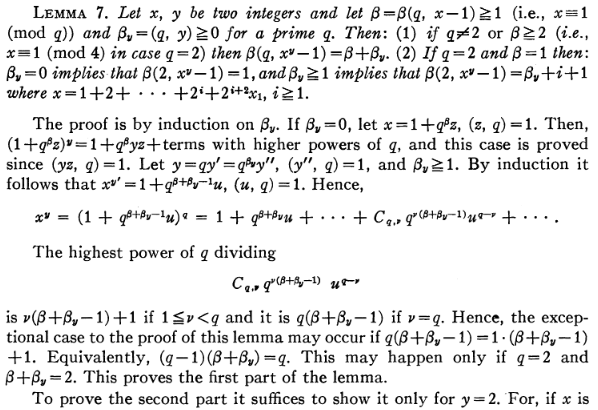

Summary of Amitsur's result
The following construction $D=(E/F,\sigma,\gamma)$ is called a cyclic division algebra.
- $\DeclareMathOperator{\Gal}{Gal}$ $\DeclareMathOperator{\N}{N}$ $F$ is a number field over $\mathbb{Q}$,
- $E/F$ is a cyclic extension of degree $n$, i.e. the field extension $E/F$ is Galois and the Galois group is cyclic,
- $\sigma$ is a generator of the cyclic group $\Gal(E/F)$ and
- $\gamma \in F^{*}$, with the property that the multiplicative order of $\gamma$ in the group $K^{*}/ N_{F}^{E}(E^{*})$ is exactly $n$. That is, $\gamma^{k} \notin N_{F}^{E}(E^{*})$ for any $k \in \{ 1,2,\dots,n-1\}$ and $\gamma^{n} = N_{F}^{E}(x)$ for some $x\in E^{*}$.
When this happens we say that $\gamma \in F^{*}$ is a non-norm element.
Consider a formal element $b$ that does not commute with $E$ and satisfies $b^{n} = \gamma$. $D$ is now defined as per the isomorphism \begin{align} \label{eq:iDentify} D \simeq E \oplus E b \oplus E b^{2} \oplus \dots \oplus E b^{n-1},\end{align} with the rule that \begin{align} bl = \sigma(l)b \text{ for all }l \in E.\label{eq:ruleofD} \end{align}
If $\gamma$ does not satisfy the non-norm condition, then we call $(E/F,\sigma,\gamma)$ just a cyclic algebra.
All division algebras over $\mathbb{Q}$ are cyclic division algebras!
The dimension of $D=(E/F,\sigma,\gamma)$ over $\mathbb{Q}$ is $\dim_{\mathbb{Q}}D = [F:\mathbb{Q}]n^2 = [E:\mathbb{Q}]n$.
For $1 \le r \le m $ and $(m,r)=1$, consider the integers
- $\DeclareMathOperator{\ord}{ord} n = \ord_{m} r$ is the multiplicative order or $r$ modulo $m$, that is the smallest postive integer $k$ such that $m \mid r^{k}-1$,
- $s = \gcd(r-1,m)$,
- $t = m/s$.
When $r=1$, we will assume $n=s=1$. In these definitions, we will think of $m$ and $r$ as two parameters and $n,s,t$ will automatically be set as defined above.
With this, consider the cyclic algebra $\mathfrak{U}_{m,r} = (\mathbb{Q}(\mu_{m}), F , \sigma_{r}, \mu_{m}^{t} )$, where $F$ is the subfield of $\mathbb{Q}(\mu_{m})$ fixed by $\sigma_{r}$, and $\sigma_{r}$ is the field automorphism of $\mathbb{Q}(\mu_{m})$ given by $\mu_{m} \mapsto \mu_{m}^{r}$.
A priori, $\mathfrak{U}_{m,r}$ is just a $\mathbb{Q}$-algebra which may not be a division algebra. For this to be a division algebra, we want that $\mu_{m}^{t}$ is a non-norm element of $F$.
Theorem
(Amitsur, 1955)Consider the following conditions on the numbers $m,r,n,s,t$ defined above. Then $\mathfrak{U}_{m,r}$ is a division algebra if and only if both of the following hold.
-
One of the following two conditions hold.
- $\gcd(n,t) = 1$. This implies that $\gcd(s,t) = 1$.
- $n=2n', m=2^{\alpha} m',s=2s'$, for some $\alpha \ge 2$ and $m',s',n'$ are odd numbers, such that $\gcd(n,t)=\gcd(s,t)=2$ and $ 2 ^{\alpha} \mid (r + 1) $.
-
One of the following two conditions hold.
- $n=s=2$ and $ m \mid (r +1)$.
- For every prime $ q \mid n$ there exists a prime $p \mid m$ such that if $m = p^{\alpha} m'$ with $p \nmid m'$, we get $q \nmid \ord_{m'} r $. In addition, at least one of the following must hold regarding $p,q$.
- $p \neq 2$ and $\gcd(q,\frac{ p^{ \delta} - 1}{s} ) = 1$, where $\delta = \ord_{m'} p$.
- $p=q=2$ and $m/4 \equiv \delta \equiv 1 \pmod{2}$, where $\delta$ is as above.
The division algebra $\mathfrak{U}_{m,r}$ contains the following group.
\begin{align} G_{m,r}:= \langle A,B \ | \ A^{m} = 1, B^{n} = A^{t}, BAB^{-1} = A^{r}\rangle. \end{align} We get that $|G_{m,r}|= mn = m \ord_{m}r$. When $r=1$, $G_{m,r}$ is a cyclic group of order $m$.
It embeds as per $i:G_{m,r} \rightarrow \mathfrak{U}_{m,r}^{*}$ defined sending $A \mapsto \mu_{m}$ and $B \mapsto b$.
When $\ord_m 2$ is odd, one can get a slightly better group of size $24 |G_{m,r}|$ embedded in the division algebra $\left(\tfrac{-1,-1}{\mathbb{Q}}\right) \otimes_{\mathbb{Q}} \mathfrak{U}_{m,r}$.
Amitsur then proves that apart from two more sporadic examples, these two are the only families of examples.
Theorem
(Amitsur, 1955)The following is an exhaustive list of finite groups \(G_{0}\) that can be embedded in some \(\mathbb{Q}\)-division algebra \(D\).
| Group structure | Conditions on the parameters | Size of the group | Dimension of the smallest division algebra containing the group |
| \(G_{0} \subseteq D^{*}\) | \(\#G_{0}\) | \(\dim_{\mathbb{Q}} \mathbb{Q}\langle G_{0}\rangle\) | |
| \(\mathfrak{D}^{*}\) | \(48\) | \(16\) | |
| \(\mathfrak{I}^{*}\) | \(120\) | \(20\) | |
| \(G_{m,r}\) | \( (m,r) = 1, \) \( \mathfrak{U}_{m,r}\) is a division algebra | \(m\ord_{m} r\) | \(\varphi(m) \ord_{m} r\) |
| \(\mathfrak{T}^{*} \times G_{m,r}\) | \(\ord_{m} 2\) is odd and the rest as above | 24 \(m\ord_{m} r\) | 4 \(\varphi(m) \ord_{m} r\) |
Here \(\mathfrak{T}^{*}, \mathfrak{D}^{*}, \mathfrak{I}^{*}\) are the binary tetrahedral group, binary octahedral group and binary icosahedral group respectively. They are finite groups whose respective size is 24,48 and 120.
Note that in the two families, $ \# G_0 / \dim_{\mathbb{Q}} \mathbb{Q} \langle G_0 \rangle = m/\varphi(m) $ or $6 m / \varphi(m)$. Looking at this, we can conclude that along no sequence of new constructions will we get $c_d > O(d \log \log d)$.
We can leverage the second family to get a sequence that shows that $c_d \ge O(d (\log \log d)^{7/24})$
$\DeclareMathOperator{\ord}{ord}$ We pick $$m = \prod_{ \substack{ p \text{ is prime} \\ p \le x \\ 2 \nmid \ord_{p} 2} }^{} p$$ and $r=1$. Then observe that with this, we get that $m$ is odd and $\ord_{m}2$ is also odd. Using the classification just given before, we get that $c_{8\varphi(m)} \ge 24m$. This sequence was the one picturized previously.
The following is also an interesting sequence made of new examples.
Let $\{ p_1,p_2,\dots\}$ be the sequence of all primes and suppose $q= 1+\prod_{i=1}^{N}p_{i} $ is a prime for some $N$. Then we can choose an integer $r$ such that $r \equiv 1 \pmod{p_i}$ for each $i$ but has $\ord_{q} r = q-1$, i.e. $r$ is a generator of $\mathbb{F}_{q}^{*}$.
Set $m=q(q-1) = q \prod_{i=1}^{N} p_i$. Then, one can check that $\mathfrak{U}_{m,r}$ is a division algebra so we can have $$ c_{2 (q-1)^{2}\varphi(q-1) } \ge q(q-1)^{2}.$$ If there are infinitely many such primes, then this sequence asymptotically approaches $O(d\log \log d)$.
Summary: Amitsur's work allows us to conclude that there are no asymptotic improvements possible when we allow some non-commutative symmetries.
Effectiveness
These results prove existence of a lattice with a high packing density. Can we actually construct such lattices algorithmically?
Theorem
(G., Vlad Serban, 2021)Let $D$ be a finite-dimensional division algebra over $\mathbb{Q}$. Let $\mathcal{O} \subseteq D$ be an order in $D$ and $G_{0} \subseteq \mathcal{O}$ be a finite group embedded in the multiplicative group of $D$. Then in $d=2\dim_{\mathbb{Q}}D$ dimensional real space, there exists a finite time algorithm to construct a lattice $\Lambda \subseteq \mathbb{R}^d$ such that the packing density of $\Lambda $ is at least \begin{align} \tfrac{1}{2^d} \# G_{0} - \varepsilon, \text{ for every }\varepsilon . \end{align}
The approach is based on methods of Moustrou (2017). The idea is that $\int_{Y_d} \Phi_f$ can be approximated by averaging $\Phi_f$ over a growing family of finitely many lattices.
Thank you for your attention!
Email:
nihar.gargava@epfl.ch
arxiv:
2107.04844
Slides:
nihargargava.com/divalg_seminar
How does it work?:
This presentation and all the animations are written in html and javascript using reveal.js and d3.js.
Feel free to contact for questions/comments.
Appendix: How to generate random 2-dimensional lattices
To the map $\psi:[\pi/3,2\pi/3]\times ]0,1] \rightarrow \mathbb{H}$
given by $\psi(a,b) = \cos(a) + i \sin(a)/b$ is a measure preserving map!
It maps the rectangle bijectively to a fundamental domain of $\mathbb{H}/SL_2(\mathbb{Z})$.
Using this, the following map randomly generates a lattice.
\[ \psi_1: [0,2\pi]\times [\pi/3,2\pi/3] \times ] 0,1] \to SL_2(\mathbb{R})\\
\psi_1(x,y,z) = \left[ \begin{smallmatrix} 1 & \cos(y) \\ 0 & 1 \end{smallmatrix} \right] \left[ \begin{smallmatrix} \left(\frac{\sin(y)}{z}\right)^{\frac{1}{2}} & 0 \\ 0 & \left({\frac{\sin(y)}{z}}\right)^{-\frac{1}{2}} \end{smallmatrix} \right] \left[ \begin{smallmatrix} \cos(x) & \sin(x) \\ -\sin(x) & \cos(x) \end{smallmatrix} \right]
\]
This only works for $d=2$. It is not known how to generalize this to higher dimensions!